二叉树

hello算法

概念

• 根节点（root node）：位于二叉树顶层的节点，没有父节点。
• 叶节点（leaf node）：没有子节点的节点，其两个指针均指向 None 。
• 边（edge）：连接两个节点的线段，即节点引用（指针）。
• 节点所在的层（level）：从顶至底递增，根节点所在层为 1 。
• 节点的度（degree）：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。
• 二叉树的高度（height）：从根节点到最远叶节点所经过的边的数量。
• 节点的深度（depth）：从根节点到该节点所经过的边的数量。
• 节点的高度（height）：从距离该节点最远的叶节点到该节点所经过的边的数量。

遍历

广度优先遍历

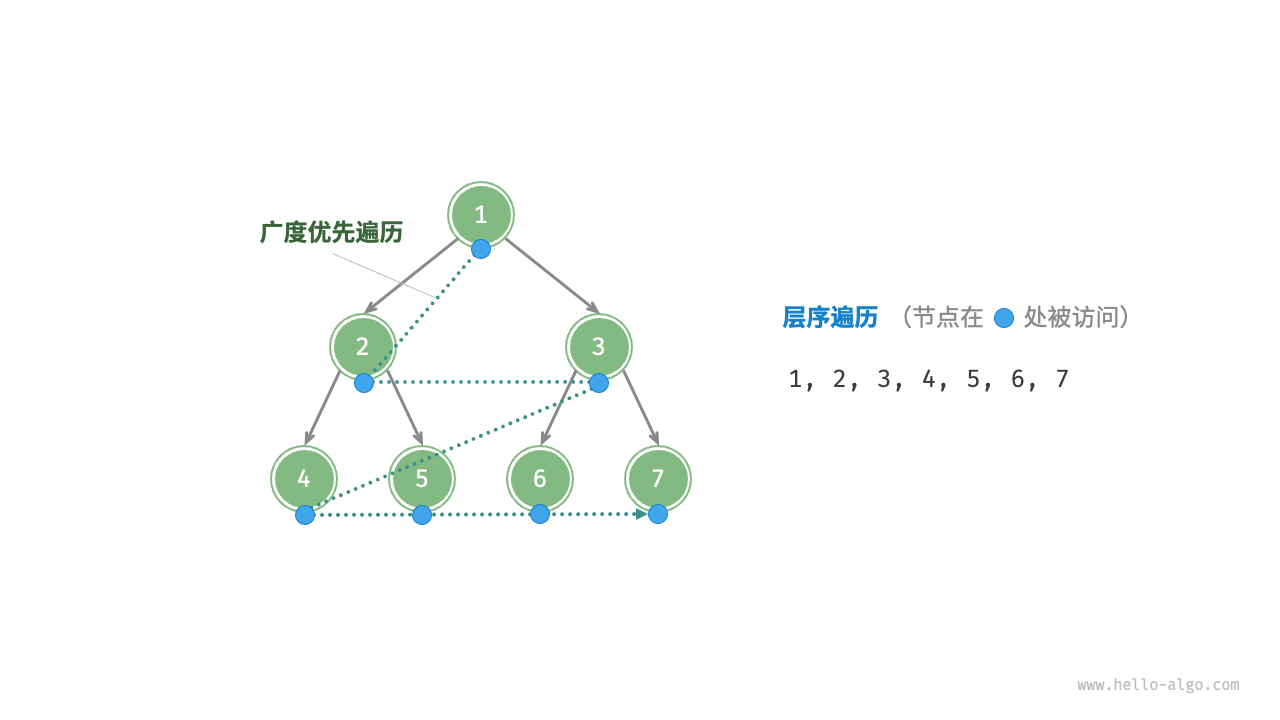
/* 层序遍历 */
vector<int> levelOrder(TreeNode *root) {
    // 初始化队列，加入根节点
    queue<TreeNode *> queue;
    queue.push(root);
    // 初始化一个列表，用于保存遍历序列
    vector<int> vec;
    while (!queue.empty()) {
        TreeNode *node = queue.front();
        queue.pop();              // 队列出队
        vec.push_back(node->val); // 保存节点值
        if (node->left != nullptr)
            queue.push(node->left); // 左子节点入队
        if (node->right != nullptr)
            queue.push(node->right); // 右子节点入队
    }
    return vec;
}

队列是一层层的堆叠并往后释放

到最后为空的时候就剩下最外层

深度优先遍历

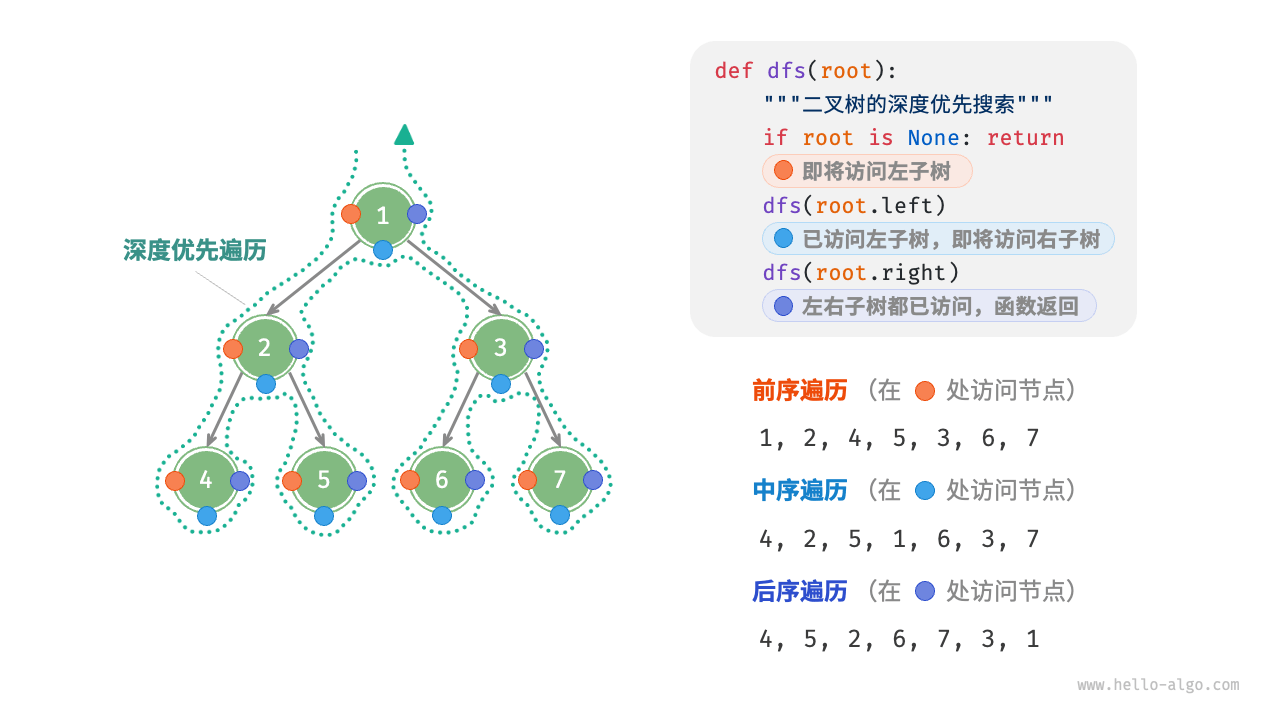
递归实现

/* 前序遍历 */
void preOrder(TreeNode *root) {
    if (root == nullptr)
        return;
    // 访问优先级：根节点 -> 左子树 -> 右子树
    vec.push_back(root->val);
    preOrder(root->left);
    preOrder(root->right);
}

/* 中序遍历 */
void inOrder(TreeNode *root) {
    if (root == nullptr)
        return;
    // 访问优先级：左子树 -> 根节点 -> 右子树
    inOrder(root->left);
    vec.push_back(root->val);
    inOrder(root->right);
}

/* 后序遍历 */
void postOrder(TreeNode *root) {
    if (root == nullptr)
        return;
    // 访问优先级：左子树 -> 右子树 -> 根节点
    postOrder(root->left);
    postOrder(root->right);
    vec.push_back(root->val);
}

遍历实现

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int val, TreeNode *left, TreeNode *right) {
        this->val = val;
        this->left = left;
        this->right = right;
    }
    TreeNode(int val):left(nullptr), right(nullptr){this->val = val;}
};

vector<int> preOeder(TreeNode *root){
    vector<int> vec;
    stack<TreeNode *> s; // 深度优先遍历到底层后需要回溯
    //回溯时由底层向上层，先进后出，故采用栈存储
    if(!root) return vec;
    s.push(root);
    while(!s.empty()){
        TreeNode *curr = s.top();
        vec.push_back(curr->val); // 这里表示先访问了根节点
        s.pop();
        // 这里压栈的顺序要注意，栈是先进后出的，因此应该先压右子树
        // 栈永远会储存上一个节点从而让搜索回溯
        if(curr->right){
            s.push(curr->right);
        }
        if(curr->left){
            s.push(curr->left);
        }
    }
    return vec;
}

vector<int> inOrder(TreeNode *root){
    vector<int> vec;
    stack<TreeNode *> s;
    if(!root) return vec;
    TreeNode *curr = root;
    while(!s.empty() || curr){ // 增加curr判断条件，因为遍历了根节点后栈为空
        // 但此时右子树尚未遍历，此时curr为右子树的根节点
        // 先把当前根节点的左子树遍历了
        while(curr){
            s.push(curr);// 这里存的对应curr->right来说是上上个节点，可以回溯
            curr = curr->left;
        }
        curr = s.top(); // 左子树遍历完毕，这里可以访问根节点
        vec.push_back(curr->val);
        s.pop();
        // 转向处理右子树
        curr = curr->right;
    }
    return vec;
}

// 双栈法
vector<int> postOrder1(TreeNode *root){
    vector<int> vec;
    stack<TreeNode *> s1; // 用于存储待处理根节点的左右节点
    stack<TreeNode *> s2; // 用于存储根节点，用于反转输出顺序
    if(!root) return vec;
    s1.push(root);
    while(!s1.empty()){
        TreeNode *curr = s1.top();
        s1.pop();
        s2.push(curr); // 此时curr就是一个根节点，直接入栈s2
        // 先入s2表示后输出，因此s1先入左子树节点，再入右子树节点，保证取出curr时是右子树节点先入s2
        if(curr->left){
            s1.push(curr->left);
        }
        if(curr->right){
            s1.push(curr->right);
        }
    }
    // 取出s2的元素赋值给vec
    while(!s2.empty()){
        TreeNode *node = s2.top();
        s2.pop();
        vec.push_back(node->val);
    }
    return vec;
}

// 一个栈+状态
vector<int> postOrder2(TreeNode *root){
    vector<int> vec;
    stack<TreeNode *> s;
    if(!root) return vec;
    TreeNode *curr = root;
    TreeNode *lastVisited = nullptr; // 记录最近访问过的节点
    while (!s.empty() || curr)
    {
        // 先将根节点及其左子树压入栈
        while(curr){
            s.push(curr);
            curr = curr->left;
        }
        curr = s.top();
        // 如果当前节点的右子树为空或者已经被访问，则访问该节点
        if(!curr->right || curr->right == lastVisited){
            s.pop();
            vec.push_back(curr->val);
            lastVisited = curr; // 更新被访问的节点
            curr = nullptr; // 准备弹出下一个节点
        } else{
            // 转向处理右子树
            curr = curr->right;
        }
    }
    return vec;
}

完美二叉树

前面都是以链表的形式来实现树

而在完美二叉树的情况下可以使用数组下标来实现访问

但是要求为完美二叉树，也就是哪怕没节点也要一个占位符

来实现父节点索引与子节点索引之间的“映射公式”：

若某节点的索引为 i ，则该节点的左子节点索引为 2i+1 ，右子节点索引为 2i+2

因此可以通过数组下标来访问或遍历节点

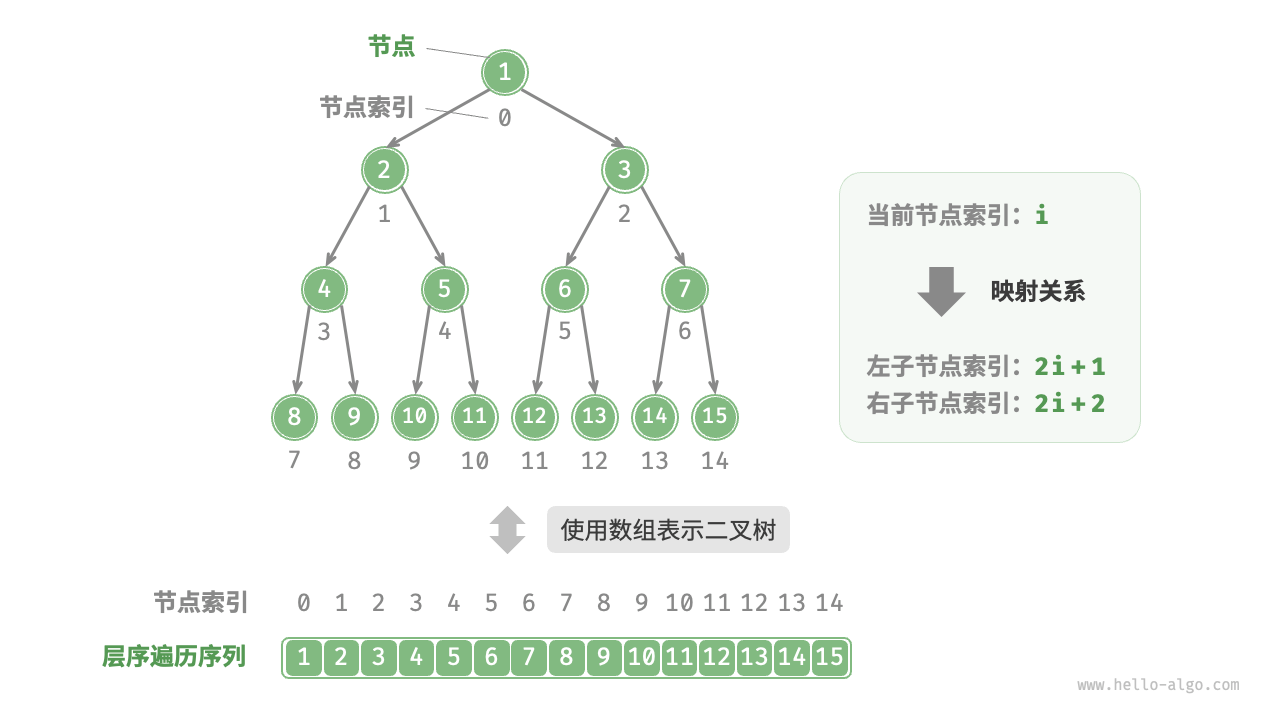
内存在连续空间中，所以相对快

/* 数组表示下的二叉树类 */
class ArrayBinaryTree {
  public:
    /* 构造方法 */
    ArrayBinaryTree(vector<int> arr) {
        tree = arr;
    }

    /* 列表容量 */
    int size() {
        return tree.size();
    }

    /* 获取索引为 i 节点的值 */
    int val(int i) {
        // 若索引越界，则返回 INT_MAX ，代表空位
        if (i < 0 || i >= size())
            return INT_MAX;
        return tree[i];
    }

    /* 获取索引为 i 节点的左子节点的索引 */
    int left(int i) {
        return 2 * i + 1;
    }

    /* 获取索引为 i 节点的右子节点的索引 */
    int right(int i) {
        return 2 * i + 2;
    }

    /* 获取索引为 i 节点的父节点的索引 */
    int parent(int i) {
        return (i - 1) / 2;
    }

    /* 层序遍历 */
    vector<int> levelOrder() {
        vector<int> res;
        // 直接遍历数组
        for (int i = 0; i < size(); i++) {
            if (val(i) != INT_MAX)
                res.push_back(val(i));
        }
        return res;
    }

    /* 前序遍历 */
    vector<int> preOrder() {
        vector<int> res;
        dfs(0, "pre", res);
        return res;
    }

    /* 中序遍历 */
    vector<int> inOrder() {
        vector<int> res;
        dfs(0, "in", res);
        return res;
    }

    /* 后序遍历 */
    vector<int> postOrder() {
        vector<int> res;
        dfs(0, "post", res);
        return res;
    }

  private:
    vector<int> tree;

    /* 深度优先遍历 */
    void dfs(int i, string order, vector<int> &res) {
        // 若为空位，则返回
        if (val(i) == INT_MAX)
            return;
        // 前序遍历
        if (order == "pre")
            res.push_back(val(i));
        dfs(left(i), order, res);
        // 中序遍历
        if (order == "in")
            res.push_back(val(i));
        dfs(right(i), order, res);
        // 后序遍历
        if (order == "post")
            res.push_back(val(i));
    }
};

二叉搜索树

使用二分法的思想，要求每个节点的序号要按照一定的规律

1. 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
2. 任意节点的左、右子树也是二叉搜索树，即同样满足条件 1. 。

搜索是对节点序号的快速定位搜索

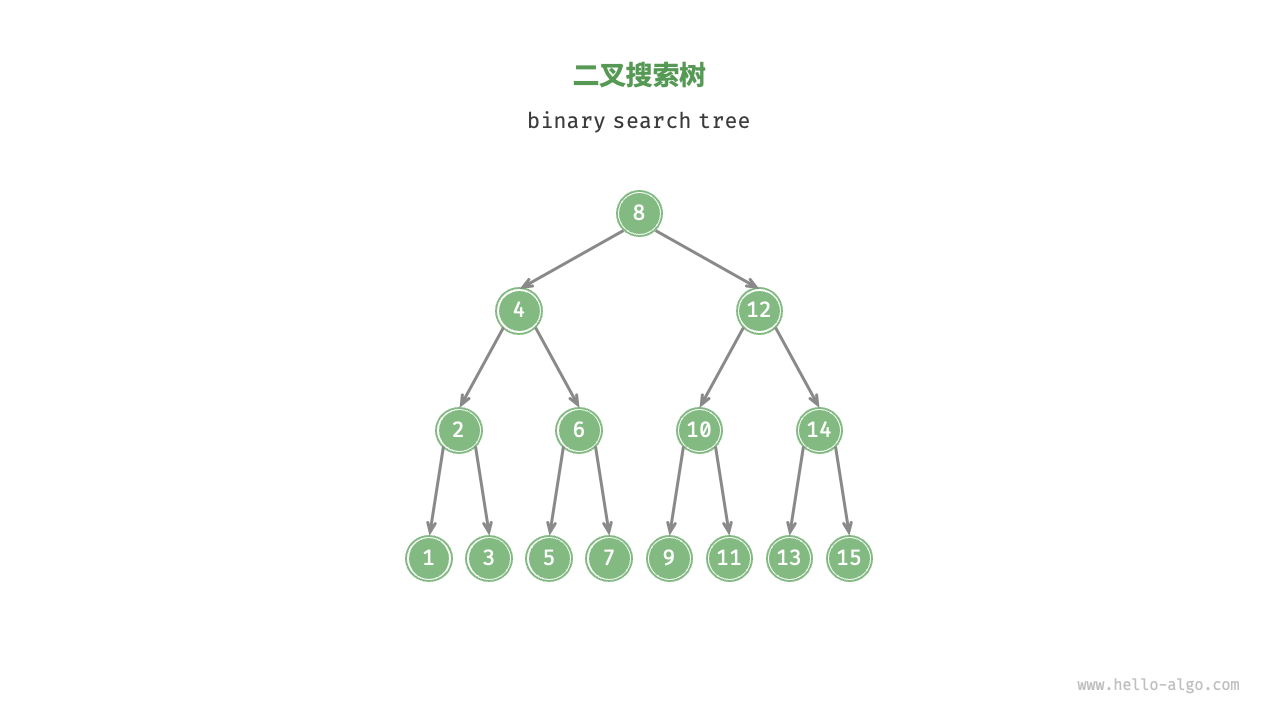
而弊端也很直观，当进行过多的增加或者删改时会导致退化，

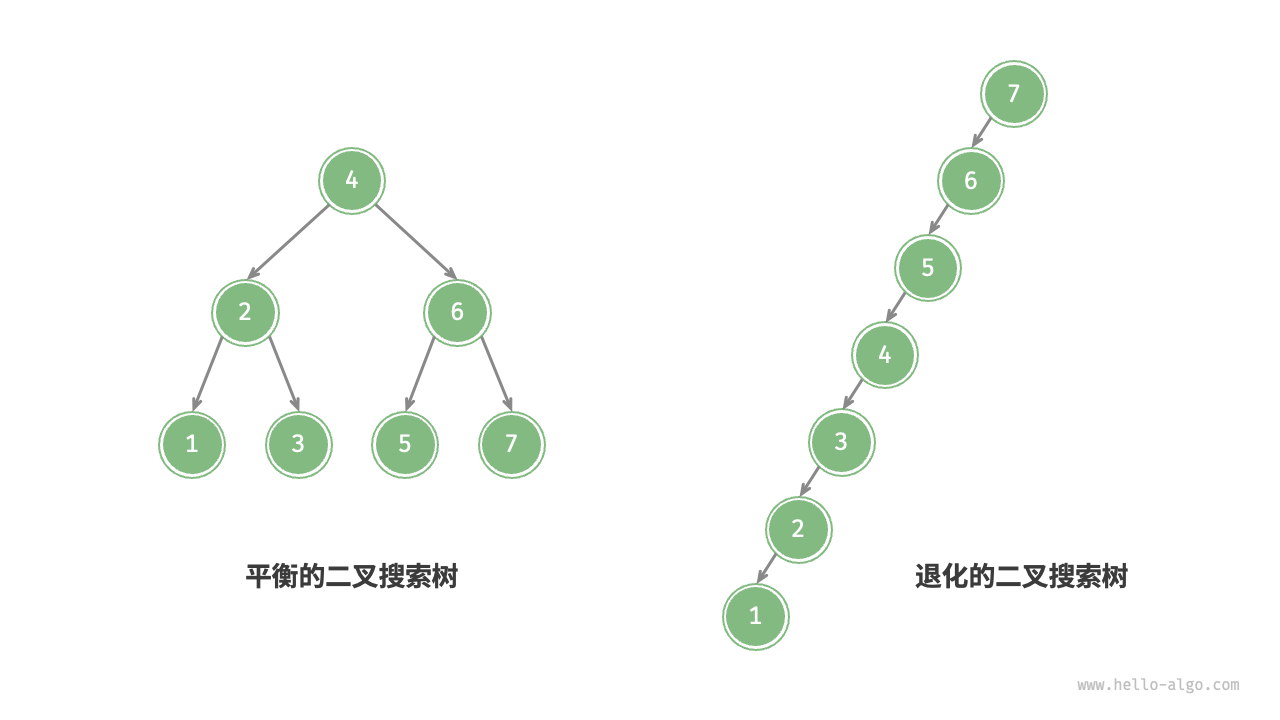
因此现在大部分都是使用红黑树或AVL等，数据量变化越快越不适合使用这个方法，感觉普通的应该只适合普通数组的索引（)

cur->val是对应节点的标记

查找

/* 查找节点 */
TreeNode *search(int num) {
    TreeNode *cur = root;
    // 循环查找，越过叶节点后跳出
    while (cur != nullptr) {
        // 目标节点在 cur 的右子树中
        if (cur->val < num)
            cur = cur->right;
        // 目标节点在 cur 的左子树中
        else if (cur->val > num)
            cur = cur->left;
        // 找到目标节点，跳出循环
        else
            break;
    }
    // 返回目标节点
    return cur;
}

插入

也是先二分搜索，到最后面发现不存在可以直接插入到当前节点下（同样要遵守二叉搜索树的规律）

/* 插入节点 */
void insert(int num) {
    // 若树为空，则初始化根节点
    if (root == nullptr) {
        root = new TreeNode(num);
        return;
    }
    TreeNode *cur = root, *pre = nullptr;
    // 循环查找，越过叶节点后跳出
    while (cur != nullptr) {
        // 找到重复节点，直接返回
        if (cur->val == num)
            return;
        pre = cur;
        // 插入位置在 cur 的右子树中
        if (cur->val < num)
            cur = cur->right;
        // 插入位置在 cur 的左子树中
        else
            cur = cur->left;
    }
    // 插入节点
    TreeNode *node = new TreeNode(num);
    if (pre->val < num)
        pre->right = node;
    else
        pre->left = node;
}

删除

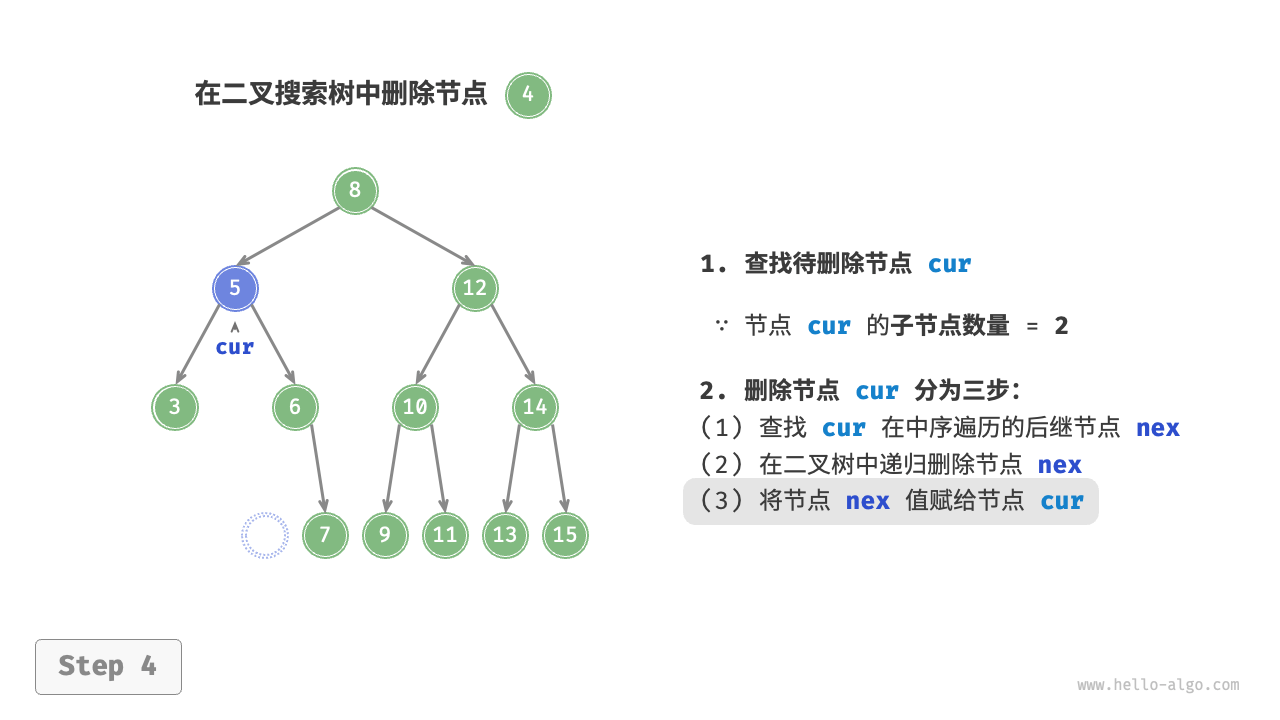
当待删除节点的度为 2 时，我们无法直接删除它，而需要使用一个节点替换该节点。由于要保持二叉搜索树“左子树 < 根节点 < 右子树”的性质，因此这个节点可以是右子树的最小节点或左子树的最大节点。

下面的代码为替换为右子树的最小节点

/* 删除节点 */
void remove(int num) {
    // 若树为空，直接提前返回
    if (root == nullptr)
        return;
    TreeNode *cur = root, *pre = nullptr;
    // 循环查找，越过叶节点后跳出
    while (cur != nullptr) {
        // 找到待删除节点，跳出循环
        if (cur->val == num)
            break;
        pre = cur;
        // 待删除节点在 cur 的右子树中
        if (cur->val < num)
            cur = cur->right;
        // 待删除节点在 cur 的左子树中
        else
            cur = cur->left;
    }
    // 若无待删除节点，则直接返回
    if (cur == nullptr)
        return;

    // 上面搜到对应的要删除节点
    // 子节点数量 = 0 or 1
    if (cur->left == nullptr || cur->right == nullptr) {
        // 当子节点数量 = 0 / 1 时， child = nullptr / 该子节点
        TreeNode *child = cur->left != nullptr ? cur->left : cur->right;
        // 删除节点 cur
        if (cur != root) {
            //只有一边的时候直接将一边接上
            if (pre->left == cur)
                pre->left = child;
            else
                pre->right = child;
        } else {
            // 若删除节点为根节点，则重新指定根节点
            root = child;
        }
        // 释放内存
        delete cur;
    }
    // 子节点数量 = 2
    else {
        // 获取中序遍历中 cur 的下一个节点
        // 右子树
        TreeNode *tmp = cur->right;
        //然后一直左，拿到最小节点
        while (tmp->left != nullptr) {
            tmp = tmp->left;
        }
        int tmpVal = tmp->val;
        // 递归删除原最小节点 tmp
        remove(tmp->val);
        // 用 tmp 覆盖 cur
        cur->val = tmpVal;
    }
}

AVL树

下面按照正常文件拆开讲

结构

相比普通的二叉搜索多了height（节点的高度）用于计算平衡因子

#include <iostream>
using namespace std;

struct TreeNode {
    int val;            // 节点的值
    TreeNode* left;     // 左子节点
    TreeNode* right;    // 右子节点
    int height;         // 当前节点的高度（用于计算平衡因子）

    TreeNode(int v) : val(v), left(nullptr), right(nullptr), height(1) {}
};

基础方法

更新当前节点的高度是根据左右子节点的高度，更新当前节点的高度。

当前节点的高度 = 左右子树最大高度 + 1：

class AVLTree {//接着后面，没闭合
public:
    TreeNode* root = nullptr;

    // 获取节点高度（空节点高度为0）
    int getHeight(TreeNode* node) {
        return node ? node->height : 0;
    }

    // 计算平衡因子 = 左子树高度 - 右子树高度
    int getBalance(TreeNode* node) {
        return node ? getHeight(node->left) - getHeight(node->right) : 0;
    }

    // 更新当前节点的高度
    void updateHeight(TreeNode* node) {
        node->height = 1 + max(getHeight(node->left), getHeight(node->right));
    }

左旋右旋操作

// 【右旋】用于左左不平衡
TreeNode* rotateRight(TreeNode* y) {
    TreeNode* x = y->left;
    TreeNode* T2 = x->right;

    x->right = y;
    y->left = T2;

    updateHeight(y);
    updateHeight(x);

    return x;
}

// 【左旋】用于右右不平衡
TreeNode* rotateLeft(TreeNode* x) {
    TreeNode* y = x->right;
    TreeNode* T2 = y->left;

    y->left = x;
    x->right = T2;

    updateHeight(x);
    updateHeight(y);

    return y;
}

以左左失衡的右旋讲解

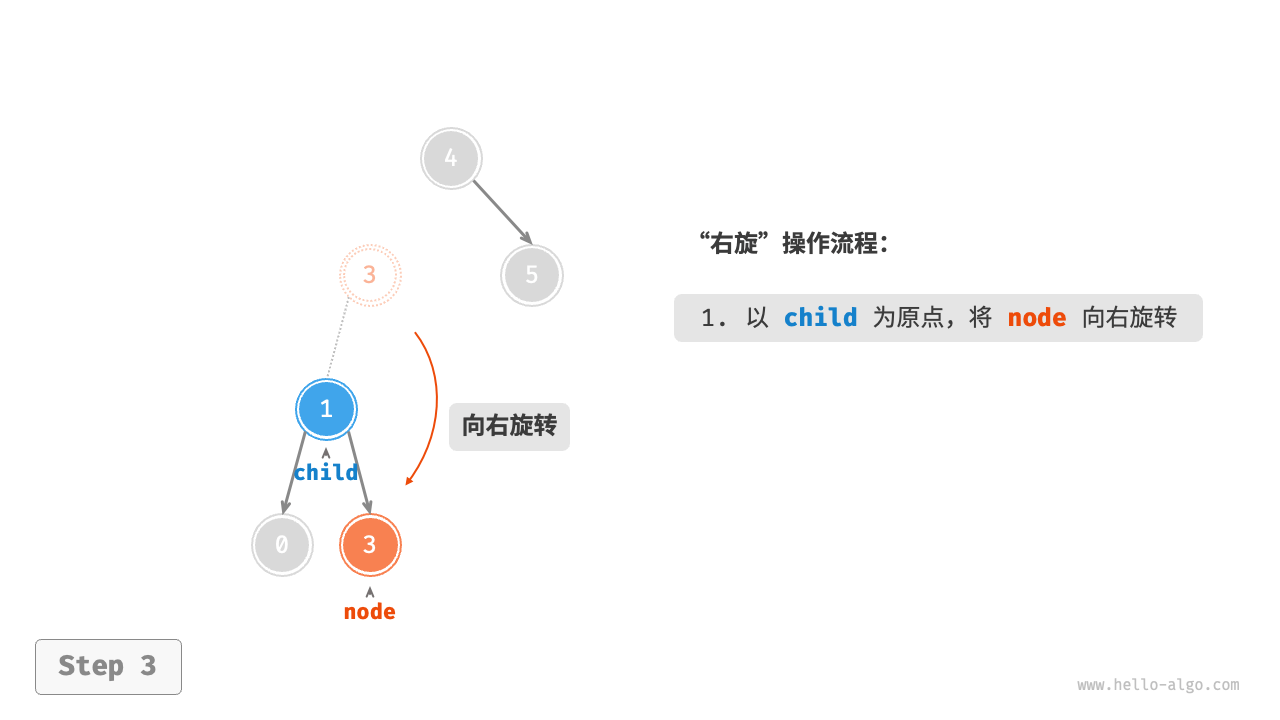
其中

TreeNode* x = y->left;
x->right = y;

理解为（旋转后y为x的右子树）

而

TreeNode* T2 = x->right;
y->left = T2;

理解为（保留原x的右子树并转移到旋转后y的左树）

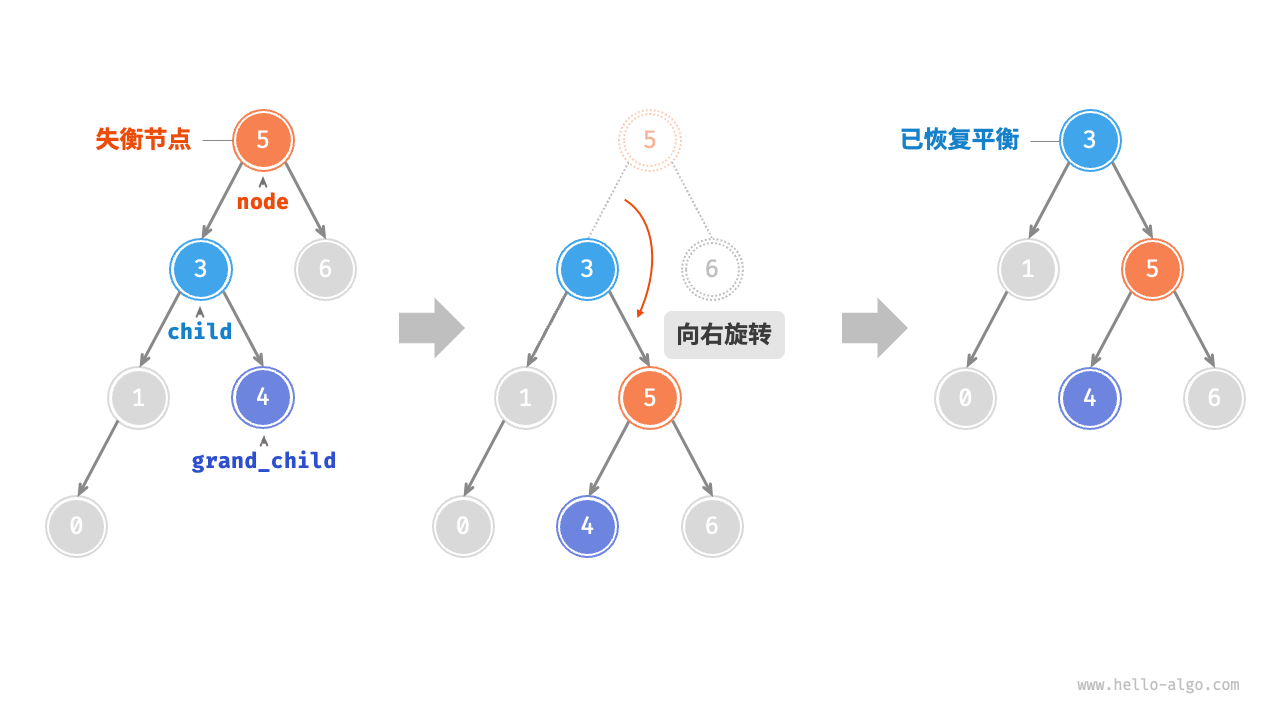
然后

return x;

理解为（返回新的根）

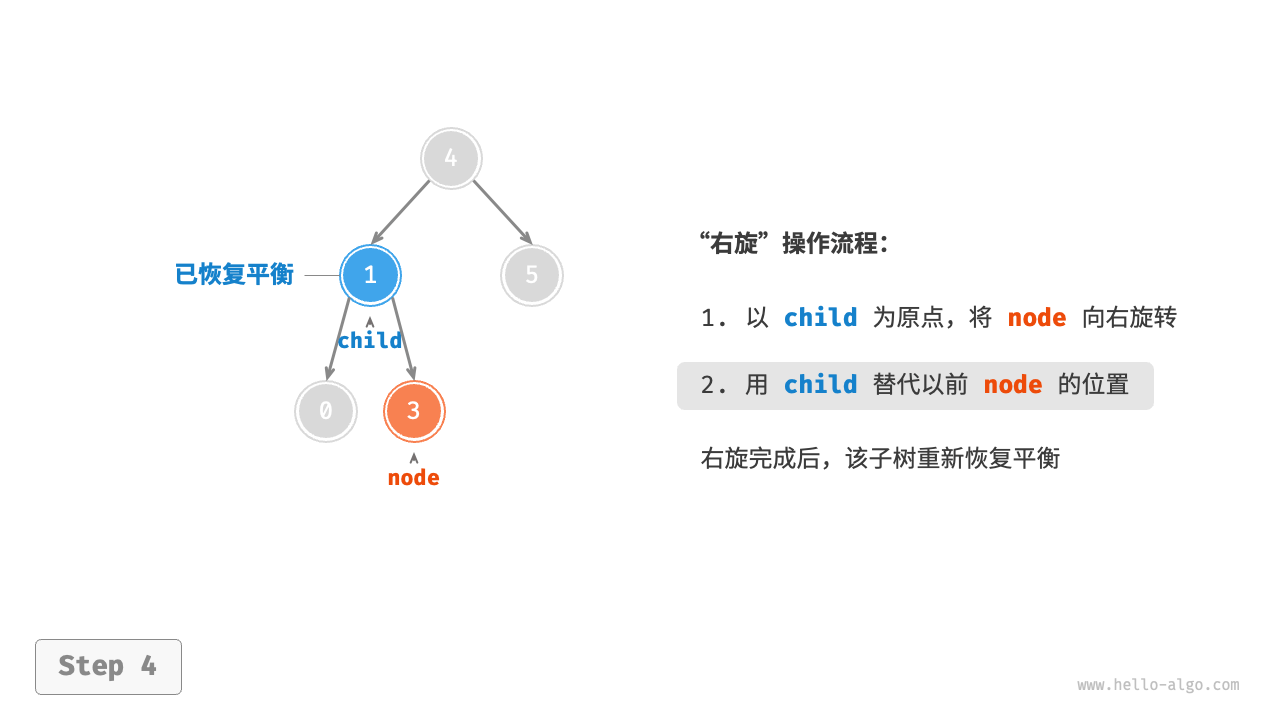
左旋反之

插入

// 插入节点并自动平衡
TreeNode* insert(TreeNode* node, int val) {
    if (!node) return new TreeNode(val);  // 新节点插入位置

    if (val < node->val) {
        node->left = insert(node->left, val);  // 插入到左子树
    } else if (val > node->val) {
        node->right = insert(node->right, val); // 插入到右子树
    } else {
        return node; // 不插入重复值
    }

    // 更新当前节点高度
    updateHeight(node);

    // 获取平衡因子，检查是否失衡
    int balance = getBalance(node);

    // 处理四种失衡情况

    // ① 左左失衡 → 右旋
    if (balance > 1 && val < node->left->val)
        return rotateRight(node);

    // ② 右右失衡 → 左旋
    if (balance < -1 && val > node->right->val)
        return rotateLeft(node);

    // ③ 左右失衡 → 左旋 + 右旋
    if (balance > 1 && val > node->left->val) {
        node->left = rotateLeft(node->left);
        return rotateRight(node);
    }

    // ④ 右左失衡 → 右旋 + 左旋
    if (balance < -1 && val < node->right->val) {
        node->right = rotateRight(node->right);
        return rotateLeft(node);
    }

    return node; // 当前节点平衡，无需旋转
}

先为正常的普通搜索二叉树插入，然后为判断是否失衡开始进行左右旋操作

通过balance < -1判断下一级是左失衡还是右失衡，也是以右为例

注意val为新插入的节点值，其在底部

1. val > node->right->val的情况下，新插入的节点在左左，因此直接rotateLeft
   显示如前面左旋右旋操作

2. val < node->right->val的情况下，新插入的节点在左右，因此要先左旋后右旋
   而先左旋旋的是新插入的节点和根节点的左节点即rotateLeft(node->left)
   左旋后就变回了左左失衡因此右旋

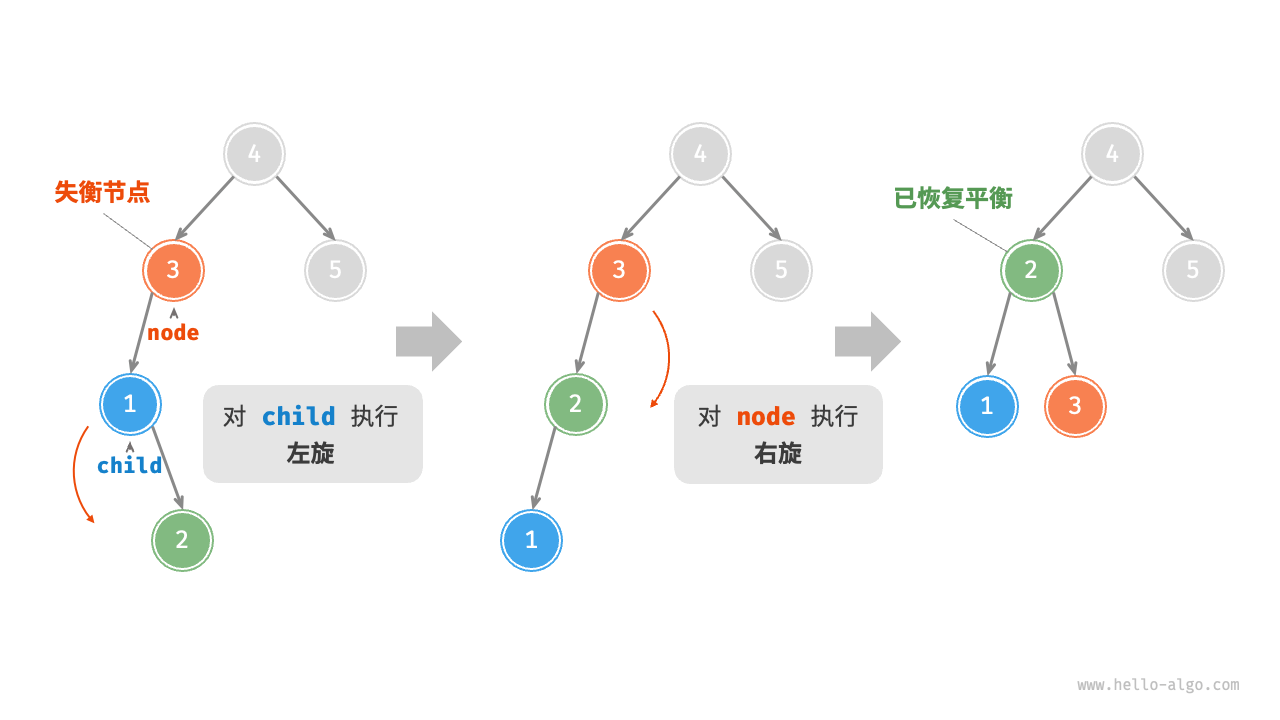
右左失衡反之

删除

和前面类似

// 查找并返回最小节点（用于删除时找中序后继）
TreeNode* getMin(TreeNode* node) {
    while (node->left)
        node = node->left;
    return node;
}

// 删除节点并自动平衡
TreeNode* remove(TreeNode* node, int val) {
    if (!node) return nullptr;

    if (val < node->val) {
        node->left = remove(node->left, val);
    } else if (val > node->val) {
        node->right = remove(node->right, val);
    } else {
        // 找到要删除的节点
        if (!node->left || !node->right) {
            TreeNode* child = node->left ? node->left : node->right;
            delete node;
            return child;
        } else {
            // 两个子节点 → 找中序后继替换
            TreeNode* successor = getMin(node->right);
            node->val = successor->val;
            node->right = remove(node->right, successor->val);
        }
    }

    updateHeight(node);
    int balance = getBalance(node);

    // 和插入一样的四种情况
    if (balance > 1 && getBalance(node->left) >= 0)
        return rotateRight(node);

    if (balance > 1 && getBalance(node->left) < 0) {
        node->left = rotateLeft(node->left);
        return rotateRight(node);
    }

    if (balance < -1 && getBalance(node->right) <= 0)
        return rotateLeft(node);

    if (balance < -1 && getBalance(node->right) > 0) {
        node->right = rotateRight(node->right);
        return rotateLeft(node);
    }

    return node;
}

查找

与前面普通二叉搜索树一致

打印遍历

   // 对外接口：插入、删除、打印
    void insert(int val) { root = insert(root, val); }
    void remove(int val) { root = remove(root, val); }
    // 打印树形结构
    void printTree(TreeNode* node, string indent = "", bool isLeft = true) {
        if (node == nullptr) return;

        if (node->right)
            printTree(node->right, indent + (isLeft ? "│       " : "        "), false);

        cout << indent;
        if (isLeft)
            cout << "└────── ";
        else
            cout << "┌────── ";
        cout << node->val<<" "<<getBalance(node) << endl;

        if (node->left)
            printTree(node->left, indent + (isLeft ? "        " : "│       "), true);
    }

    // 对外接口
    void printTree() {
        cout << "树形输出:" << endl;
        printTree(root, "", true);
    }

};//闭合

红黑树

红黑树类的定义

一棵合法的红黑树必须遵循以下四条性质：

1. 节点为红色或黑色
2. NIL 节点（空叶子节点）为黑色
3. 红色节点的子节点为黑色
4. 从根节点到 NIL 节点的每条路径上的黑色节点数量相同

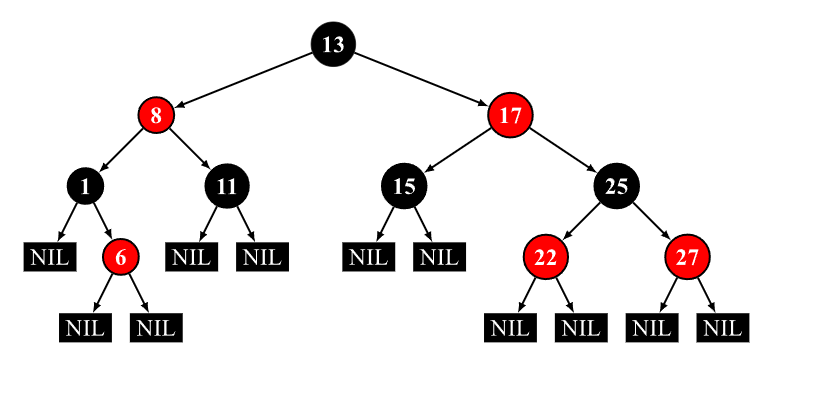
部分资料中还加入了第五条性质，即根节点必须为黑色，这条性质要求完成插入操作后若根节点为红色则将其染黑，但由于将根节点染黑的操作也可以延迟至删除操作时进行，因此，该条性质并非必须满足（本文给出的代码实现中满足该性质）。为严谨起见，这里同时引用 维基百科原文 进行说明：

Some authors, e.g. Cormen & al.,2claim "the root is black" as fifth requirement; but not Mehlhorn & Sanders3or Sedgewick & Wayne.4Since the root can always be changed from red to black, this rule has little effect on analysis. This article also omits it, because it slightly disturbs the recursive algorithms and proofs.

AVL vs 红黑树

特性	AVL 树	红黑树
平衡原则	严格的高度平衡（左右高差 ≤ 1）	相对平衡（通过黑高与颜色规则）
插入触发	只要高度失衡立即旋转	只在“红红冲突”或黑高不一致时旋转与染色
删除触发	结构失衡立即旋转	更复杂，通常惰性修复
性能	查询快但插入、删除频繁时较慢	插入删除更快，查询略劣
实现复杂度	中等	较高（颜色规则 + 多种修复情况）

结构

相对于AVL而言，红黑树使用的是Color（颜色标记）和parent（访问父节点）

#include <iostream>
using namespace std;

enum Color { RED, BLACK };

struct Node {
    int val;
    Color color;
    Node *left, *right, *parent;
    Node(int v) : val(v), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
};

左旋右旋操作

使用指向父节点的指针实现旋转，实现原理类似

就是要注意维护parent一直指向父节点，每一个都要改

class RedBlackTree {//未闭合
public:
    Node* root = nullptr;
    void rotateLeft(Node* x) {
        Node* y = x->right;
        x->right = y->left;
        if (y->left) y->left->parent = x;
        y->parent = x->parent;
        if (!x->parent) root = y;
        else if (x == x->parent->left) x->parent->left = y;
        else x->parent->right = y;
        y->left = x;
        x->parent = y;
    }

    void rotateRight(Node* y) {
        Node* x = y->left;
        y->left = x->right;
        if (x->right) x->right->parent = y;
        x->parent = y->parent;
        if (!y->parent) root = x;
        else if (y == y->parent->right) y->parent->right = x;
        else y->parent->left = x;
        x->right = y;
        y->parent = x;
    }

插入

void insert(int val) {
    Node* node = new Node(val);//建立新节点
    root = bstInsert(root, node);
    fixViolation(node);// 插入后按照规则修复
}

Node* bstInsert(Node* r, Node* node) {
    if (!r) return node;
    if (node->val < r->val) {
        r->left = bstInsert(r->left, node);
        r->left->parent = r; // 要指定父节点
    } else {
        r->right = bstInsert(r->right, node);
        r->right->parent = r; // 要指定父节点 
    }
    return r;
}

插入修复

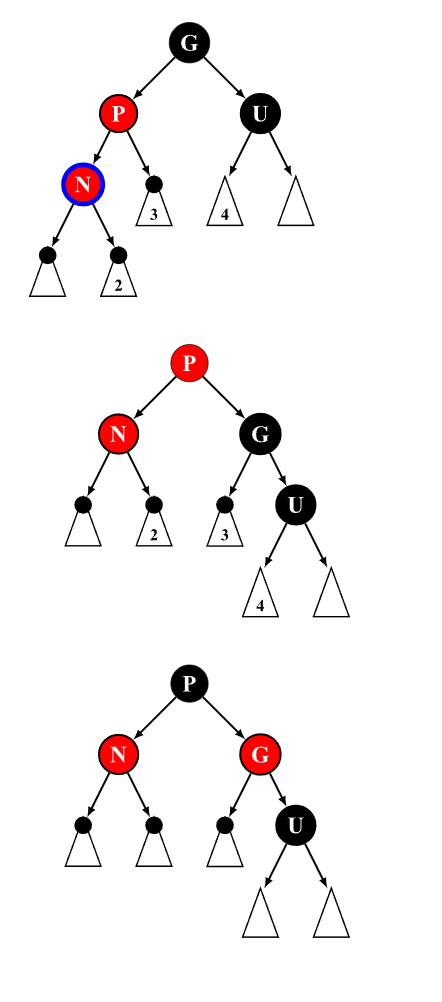
情况 1：父红 + 叔红 → 重新着色，上移问题；

情况 2：父红 + 叔黑 + 当前节点“在弯处” → “先旋直”；

情况 3：当前节点“在直线上” → 旋转+染色；

    void fixViolation(Node* node) {
        // 只要当前节点不是根，并且其父亲是红色，就可能违反红黑树“红色不能相连”规则
        while (node != root && node->parent && node->parent->color == RED) {
            Node* parent = node->parent;        // 父节点
            Node* gp = parent->parent;          // 父父 == 爷节点（祖父节点）

            // 父节点是爷节点的左孩子
            if (parent == gp->left) {
                Node* uncle = gp->right;        // 叔叔 = 爷的右子节点

                // 情况1：叔叔存在且为红色 → 祖父下的两个孩子都红，变色即可
                if (uncle && uncle->color == RED) {
                    parent->color = BLACK;      // 父变黑
                    uncle->color = BLACK;       // 叔变黑
                    gp->color = RED;            // 爷变红（往上传递红冲突）
                    node = gp;                  // 继续向上检查爷是否也违反规则
                } else {
                    // 情况2/3：叔叔不存在 或 为黑色 → 需旋转修复
                    // 情况2：当前节点是右子 → 左旋父节点，变成情况3
                    if (node == parent->right) {
                        rotateLeft(parent);     // 左旋父节点，使 node 成为直线结构
                        node = parent;          // 更新当前节点位置
                        parent = node->parent;  // 同步更新 parent
                    }

                    // 情况3：当前节点是左子 → 对爷节点右旋，父变黑，爷变红
                    rotateRight(gp);            // 对爷右旋，修复结构
                    parent->color = BLACK;  // 直接设置颜色，而非交换
                    gp->color = RED;
                    node = gp;  // 将node设为祖父节点以继续检查
                }

            } else {
                // 对称逻辑：父节点是爷节点的右孩子
                Node* uncle = gp->left;         // 叔叔 = 爷的左子节点

                // 情况1（对称）：叔叔红 → 变色 + 向上继续
                if (uncle && uncle->color == RED) {
                    parent->color = BLACK;
                    uncle->color = BLACK;
                    gp->color = RED;
                    node = gp;
                } else {
                    // 情况2（对称）：当前是左子 → 右旋父，转为情况3
                    if (node == parent->left) {
                        rotateRight(parent);
                        node = parent;
                        parent = node->parent;
                    }

                    // 情况3（对称）：当前是右子 → 左旋爷 + 父变黑、爷变红
                    rotateLeft(gp);
                    parent->color = BLACK;  // 直接设置颜色，而非交换
                    gp->color = RED;
                    node = gp;  // node设为祖父节点以继续检查
                }
            }
        }

        // 最终确保根节点始终为黑色
        root->color = BLACK;
    }

如下面的就是情况2到情况3到情况1

删除

总体和前面一致

只是写法变了，而且通过transplant来维护parent始终有指向父节点

    /* 用 v 替换 u 在树中的位置（不做颜色处理） */
    void transplant(Node* u, Node* v) {
        if (!u->parent)               root = v;
        else if (u == u->parent->left) u->parent->left  = v;
        else                           u->parent->right = v;
        if (v) v->parent = u->parent;
    }

    /* 返回以 x 为根的子树中的最小节点（后继） */
    Node* minimum(Node* x) const {
        while (x && x->left) x = x->left;
        return x;
    }

    void remove(int key) {
        Node* z = root;
        while (z && z->val != key)         // 找要删除的节点 z
            z = (key < z->val) ? z->left : z->right;
        if (!z) return;                    // 若不存在，直接返回

        Node* y = z;                       // y 是最终被“真正删除”的节点
        Color yOriginalColor = y->color;

        Node* x = nullptr;                 // x 是 y 的唯一子（可能为空），用于后续修复
        Node* xParent = nullptr;           // 记录 x 的父节点

        if (!z->left) {                    // z 至多一个右孩子
            x = z->right;
            xParent = z->parent;
            transplant(z, z->right);
        } else if (!z->right) {            // z 只有左孩子
            x = z->left;
            xParent = z->parent;
            transplant(z, z->left);
        } else {                           // z 有两个孩子
            y = minimum(z->right);         // y 为 z 的后继，必无左孩子
            yOriginalColor = y->color;
            x = y->right;
            if (y->parent == z) {
                if (x) x->parent = y;      // 注意：y->right 可能为空
                xParent = y;
            } else {
                transplant(y, y->right);   // 把 y 的右子顶到 y 位置
                y->right = z->right;
                y->right->parent = y;
                xParent = y->parent;
            }
            transplant(z, y);              // 用 y 顶替 z
            y->left = z->left;
            y->left->parent = y;
            y->color = z->color;           // 保持整体黑高不变
        }
        delete z;

        /* 如果被删除节点颜色是黑，需要修复红黑性质 */
        if (yOriginalColor == BLACK)
            deleteFixup(x, xParent);//因为没用哨兵节点（空但是有颜色和指向父节点）
                                //所以要维护xParent
    }

删除修复

为4个情况，见

https://oi-wiki.org/ds/rbtree/#delete-case-1

情况 1：兄弟红 → 旋转 + 变色，转换为 Case 2/3/4；

情况 2：兄弟黑 + 两个侄子都黑 → 兄弟染红，问题上传；

情况 3：兄弟黑 + 近侄红 + 远侄黑 → 旋转 + 变色，转为 Case 4；

情况 4：兄弟黑 + 远侄红 → 旋转 + 父色传递 + 清除双黑；

/* 删除修复：
 *   x —— 最终被移动到原删除位置的“替身”节点（可能为 nullptr / NIL）
 *   p —— x 当前的父节点
 */
void deleteFixup(Node* x, Node* p) {

    // 只要 x 不是根，且 x 仍带着“双黑”（为空或黑色），就必须继续修复
    while (x != root && (x == nullptr || x->color == BLACK)) {

        /*====================  情形 A：x 是父节点 p 的左孩子  ====================*/
        if (x == p->left) {

            Node* w = p->right;                 // 兄弟节点（p 的右孩子）

            /*—— Case 1：兄弟 w 为红 ——*/
            if (w && w->color == RED) {
                w->color = BLACK;               // 兄弟染黑
                p->color = RED;                 // 父染红
                rotateLeft(p);                  // 对父进行左旋，使 w 变为新的父
                w = p->right;                   // 更新兄弟指针（此时 w 必为黑）
            }

            /* w 必为黑，下面再分侄子情况 */
            /*—— Case 2：兄弟黑，且两个侄子都黑 ——*/
            if ( (!w->left  || w->left ->color == BLACK) &&
                 (!w->right || w->right->color == BLACK) ) {

                if (w) w->color = RED;          // 兄弟染红，抵消一层黑
                x = p;                          // 双黑上移到父
                p = x->parent;                  // 同步更新 p，进入下一轮 while

            } else {                            // 至少有一个侄子为红

                /*—— Case 3：兄弟黑，近侄（左）红，远侄（右）黑 ——*/
                if (!w->right || w->right->color == BLACK) {
                    if (w->left) w->left->color = BLACK; // 近侄染黑
                    w->color = RED;                      // 兄弟染红
                    rotateRight(w);                      // 右旋兄弟，使远侄变红
                    w = p->right;                        // 更新兄弟指针，转换为 Case 4
                }

                /*—— Case 4：兄弟黑，远侄红 ——*/
                w->color = p->color;          // 兄弟继承父的颜色
                p->color = BLACK;             // 父节点变黑
                if (w->right) w->right->color = BLACK; // 远侄染黑
                rotateLeft(p);                // 左旋父节点，消除双黑
                x = root;                     // 双黑已解决，跳出循环
                break;
            }

        /*====================  情形 B：x 是父节点 p 的右孩子  ====================*/
        } else {                               // 以下代码与上面对称，左右互换

            Node* w = p->left;                  // 兄弟 = p 的左孩子

            /*—— Case 1（对称）：兄弟红 ——*/
            if (w && w->color == RED) {
                w->color = BLACK;
                p->color = RED;
                rotateRight(p);                 // 对父右旋
                w = p->left;                    // 更新兄弟指针
            }

            /* w 为黑，继续分侄子情况 */
            /*—— Case 2（对称）：兄弟黑，两侄黑 ——*/
            if ( (!w->left  || w->left ->color == BLACK) &&
                 (!w->right || w->right->color == BLACK) ) {

                if (w) w->color = RED;
                x = p;
                p = x->parent;

            } else {

                /*—— Case 3（对称）：近侄红，远侄黑 ——*/
                if (!w->left || w->left->color == BLACK) {
                    if (w->right) w->right->color = BLACK;
                    w->color = RED;
                    rotateLeft(w);              // 左旋兄弟
                    w = p->left;                // 更新兄弟指针
                }

                /*—— Case 4（对称）：远侄红 ——*/
                w->color = p->color;
                p->color = BLACK;
                if (w->left) w->left->color = BLACK;
                rotateRight(p);                 // 右旋父节点
                x = root;                       // 退出 while
                break;
            }
        }
    }

    /* 循环结束：把最终 x 染黑，确保根-叶路径黑高统一 */
    if (x) x->color = BLACK;
}

打印遍历

    void inorder(Node* node) {
        if (!node) return;
        inorder(node->left);
        cout << node->val << (node->color == RED ? " [R]" : " [B]") << " ";
        inorder(node->right);
    }

    void printInorder() {
        inorder(root);
        cout << endl;
    }

    void printTree(Node* node, string indent = "", bool isLeft = true) {
        if (!node) return;
        if (node->right) printTree(node->right, indent + (isLeft ? "│   " : "    "), false);
        cout << indent << (isLeft ? "└── " : "┌── ") << node->val << (node->color == RED ? " [R]" : " [B]") << endl;
        if (node->left) printTree(node->left, indent + (isLeft ? "    " : "│   "), true);
    }

    void printTree() { cout << "树:" << endl;printTree(root); }

}; // 闭合